Day 9: Reading a Spectrogram

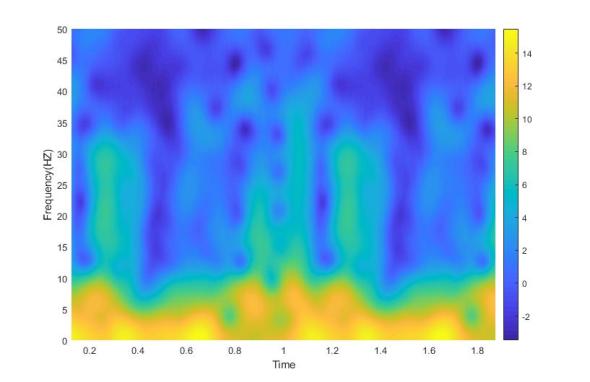
Definitely not the same spectrogram as yesterday, no really look. Now for the part where I tell you how to read this thing…
Last post we introduced a new tool in our arsenal of signal processing analysis, the spectrogram. Without knowing how to read it, it just looks sort of like a colored mess. Don’t get me wrong, it is an interesting looking colored mess, but a mess nonetheless. Well today we are going to talk about how to interpret the plot and why exactly we would ever use this seeming monstrosity.*
Day 8: The Spectrogram Function

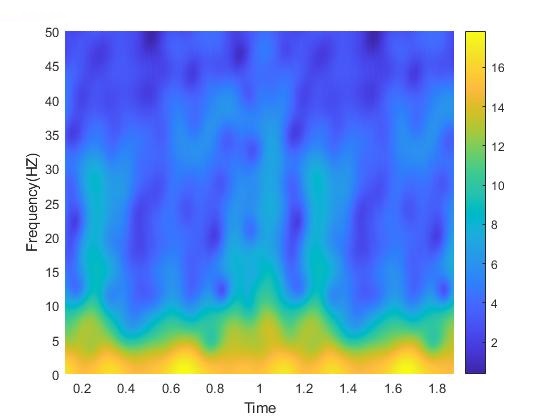
Example spectrogram from some data I had recently processed
To (somewhat) continue with our signal processing theme that we have going on at the moment, over the next few days, let’s look at something called the spectrogram. It’s three dimensions of fun!*
Day 7: Small waves, or wavelets!

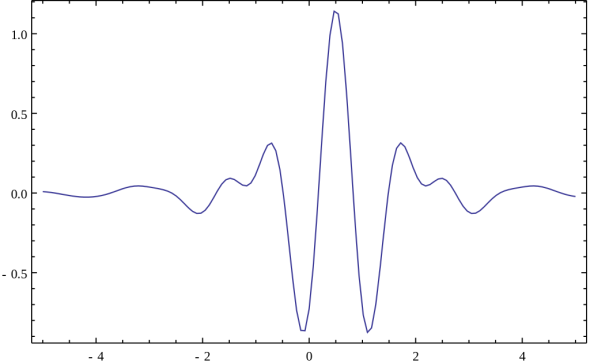
This is the Meyer wave, a representation of a so-called mother wavelet function to use for the wavelet transform. Notice that it is finite!
Waves! We’re officially one week through 365 Days of Academia! Woo! 1 week down, 51(.142…) weeks left! Let’s wrap up this weeks theme (there wasn’t originally a theme, but it kind of ended up that way) by talking about other ways we can get to the frequency domain. Specifically, let’s stop the wave puns and let’s talk wavelets!*
Day 6: The fast and the Fourier

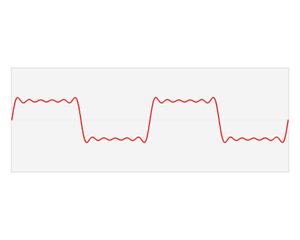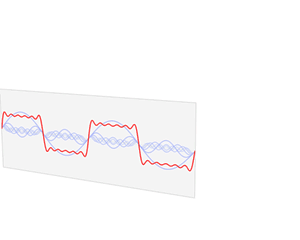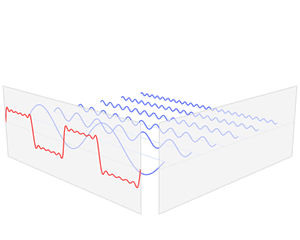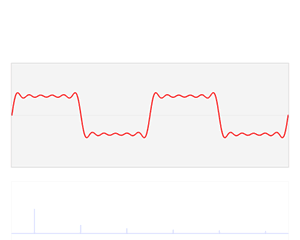
A good example of how the Fourier transform can approximate signals. The red signal is our input signal and the blue shows how the output of the Fourier transform.
Okay, if you’ve been keeping up with these posts, we know about Welch’s method, Thomson’s method, the things that make them different, and the things that make them similar. The thing that both of these transforms rely on is the Fourier transform. What is the Fourier transform? Well, something I probably should have covered first, but whatever this is my blog we do it in whatever order we feel like, so let’s dive in!*
Day 5: Whose window function is it anyway?


This is not how we use a window function on the computer…
One day someone looked at the windowed fourier transform and said, “Don’t be such a square!” and thus window functions were invented. If you believe that, then I have an island for sale, real cheap. But seriously, let’s do a dive into what a window function is and why the heck there are so many of them, because there ARE a LOT! So let’s get started!*
Day 4: Spectral leakage… embarrassing

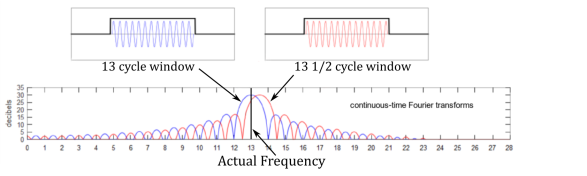
Look at that leakage!
Leakage, it’s never a good thing. For today’s post we’re going to cover a very important topic. Spectral leakage, it’s a big reason why spectral density estimation is well, an estimation. The other reason it is an estimation is because the fourier transform is an approximation of the original signal, but the Fourier transform is a whole other post on its own. So let’s talk leakage!*
Day 3: Power Spectral Density Overview

In our last post we introduced the two main characters in this story of spectrogram. On one end we have Welch’s method (pwelch) on the other end we have the Thomson multitaper method (pmtm). As promised here is a awful basic breakdown of why is more than one way to compute power spectral density (in fact there are several, far more than the two I’m talking about). So, let’s just dig right in!*
Day 2: Power Spectral Density (pmtm)

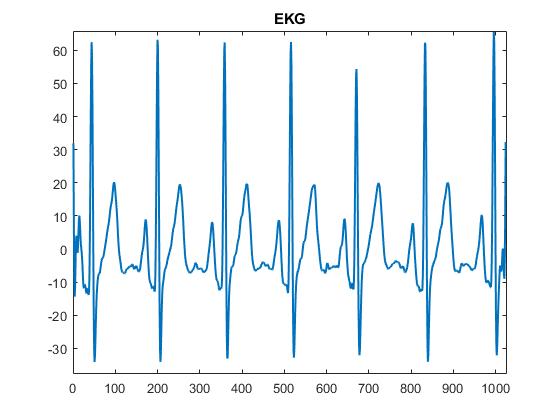
A example EKG signal
This is a (somewhat) continuation on what we were discussing in the previous post. We covered the pwelch MATLAB function, this time we will cover the PMTM function, this function uses the Thomson multitaper method to calculate power spectral density. We can do a deep dive into the differences between the two next time, but for now let’s talk about the command itself.*
Back again with 365 Days of Academia

It’s been an awful time. dusts off the cobwebs around the blog Things have been rough, but I figure it’s time to try and blog regularly again.
So what’s new?

Humanoid bipedal robot for balance testing, 100% designed and built by me!




